如何在论坛输入数学公式?--LaTex使用帮助
一、LaTex简介
LaTeX (LATEX,音译“拉泰赫”)是一种基于TeX的排版系统,由美国计算机学家莱斯利·兰伯特(Leslie Lamport)在20世纪80年代初期开发,利用这种格式,即使使用者没有排版和程序设计的知识也可以充分发挥由TeX所提供的强大功能,能在几天,甚至几小时内生成很多具有书籍质量的印刷品。对于生成复杂表格和数学公式,这一点表现得尤为突出。因此它非常适用于生成高印刷质量的科技和数学类文档。这个系统同样适用于生成从简单的信件到完整书籍的所有其他种类的文档。 (LATEX,音译“拉泰赫”)是一种基于TeX的排版系统,由美国计算机学家莱斯利·兰伯特(Leslie Lamport)在20世纪80年代初期开发,利用这种格式,即使使用者没有排版和程序设计的知识也可以充分发挥由TeX所提供的强大功能,能在几天,甚至几小时内生成很多具有书籍质量的印刷品。对于生成复杂表格和数学公式,这一点表现得尤为突出。因此它非常适用于生成高印刷质量的科技和数学类文档。这个系统同样适用于生成从简单的信件到完整书籍的所有其他种类的文档。
二、所见所得方式编辑公式
在线LaTex公式编辑器
http://www.codecogs.com/products/eqneditor/editor.php?lang=zh-cn
用上面的在线公式编辑器编辑好公式之后,复制公式代码,然后粘贴到论坛tex标签之间。
例子1.
公式代码:a^{2}+b^{2}=\int (a^{b}+c) dx
复制到tex标签中:[tex]a^{2}+b^{2}=\int (a^{b}+c) dx[/tex]
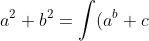 dx)
|